DES formulations
ChatGPT and Grok seem to understand DES and SA at an acceptable level.
🧩 1. Original DES (SA-DES, 1997)
Reference: Spalart, P. R., Jou, W. H., Strelets, M., & Allmaras, S. R. (1997). Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach.
- Base model: Spalart–Allmaras (RANS)
- Modification: The wall-distance term ( d ) in the destruction term of SA is replaced by \[ \tilde{d} = \min(d, C_{DES} \Delta) \] where \( \Delta \) is the local grid length scale, and \( C_{DES} \approx 0.65 \).
- Idea: When the grid spacing becomes smaller than the local boundary-layer thickness (in separated regions), the model switches to LES mode by limiting the eddy viscosity length scale.
Issue: In attached boundary layers on coarse grids, \( \Delta < d \) may occur unintentionally, causing grid-induced premature separation (“modeled-stress depletion”).
⚙️ 2. Delayed DES (DDES, 2006)
Reference: Spalart, P. R., Deck, S., Shur, M. L., Squires, K. D., Strelets, M. K., & Travin, A. (2006). A new version of detached-eddy simulation, resistant to ambiguous grid densities.
Base model: SA or SA-neg
- \[
d_{DDES} = d - f_d \max(0, d - C_{DES}\Delta)
\]
with \( f_d \to 1 \) in the boundary layer (RANS mode) and \( f_d \to 0 \) in separated flow (LES mode).
Benefit: Prevents premature activation of LES inside attached layers.
🧮 3. Improved Delayed DES (IDDES, 2009)
Reference: Shur, M., Spalart, P. R., Strelets, M., & Travin, A. (2008/2009). A hybrid RANS–LES approach with delayed-DES and wall-modeled LES capabilities.
Base model: SA or SA-neg
Modification: Refines DDES by adding:
- Improved length-scale blending for smoother RANS–LES transition.
- Explicit wall-modeling capability for high-Reynolds-number wall-bounded flows (WMLES mode).
- Dynamic filter width depending on wall distance and grid anisotropy.
Use case: Widely used in industrial CFD (e.g. ANSYS Fluent, OpenFOAM). Suitable for external aerodynamics.
Original Spalart–Allmaras (SA) Turbulence Model
With Linear Suppression Term \( f_{t2} \)
This document formulates the Spalart–Allmaras one-equation turbulence model including the linear suppression (trip) term \( f_{t2} \). The formulation is consistent with the original SA model as used in early transition-sensitive and DES-capable implementations (e.g. SA, SA-neg, SA-DES).
1. Transport Equation
The transported variable is the modified kinematic eddy viscosity \( \tilde{\nu} \).
$$ \frac{\partial \tilde{\nu}}{\partial t}+ u_j \frac{\partial \tilde{\nu}}{\partial x_j}= P_{\tilde{\nu}}- D_{\tilde{\nu}}+ \frac{1}{\sigma} \left[ \frac{\partial}{\partial x_j} \left( (\nu + \tilde{\nu}) \frac{\partial \tilde{\nu}}{\partial x_j} \right)+ C_{b2} \left( \frac{\partial \tilde{\nu}}{\partial x_j} \right)^2 \right] $$2. Production Term (with \( f_{t2} \))
\[ P_{\tilde{\nu}}= C_{b1} (1 - f_{t2}) \tilde{S} \tilde{\nu} \]The linear suppression term \( f_{t2} \) reduces turbulence production in laminar or transitional regions.
3. Modified Vorticity Magnitude
\[ \tilde{S}= S+ \frac{\tilde{\nu}}{\kappa^2 d^2} f_{v2} \]where
\[ S = \sqrt{2 \Omega_{ij} \Omega_{ij}} \]4. Destruction Term
\[ D_{\tilde{\nu}}= C_{w1} f_w \left( \frac{\tilde{\nu}}{d} \right)^2 \]5. Eddy Viscosity Relation
\[ \nu_t = \tilde{\nu} f_{v1} \]with
\[ f_{v1}= \frac{\chi^3}{\chi^3 + C_{v1}^3}, \qquad \chi = \frac{\tilde{\nu}}{\nu} \]6. Auxiliary Functions
6.1 Viscous Damping Function
\[ f_{v2}= 1- \frac{\chi}{1 + \chi f_{v1}} \]6.2 Wall Destruction Function
\[ f_w= g \left[ \frac{1 + C_{w3}^6}{g^6 + C_{w3}^6} \right]^{1/6} \]with
\[ g= r + C_{w2} (r^6 - r), \qquad r= \frac{\tilde{\nu}}{\tilde{S} \kappa^2 d^2} \]7. Linear Suppression Function \( f_{t2} \)
\[ f_{t2}= C_{t3} \exp(-C_{t4} \chi^2) \]This term:
- Appears linearly in the production term
- Suppresses turbulence growth in laminar regions
- Is typically inactive in fully turbulent flows
- Plays a role in transition-sensitive and DES/IDDES ψ-modifications
8. Model Constants
| Constant | Value |
|---|---|
| \( \sigma \) | \( 2/3 \) |
| \( C_{b1} \) | 0.1355 |
| \( C_{b2} \) | 0.622 |
| \( \kappa \) | 0.41 |
| \( C_{v1} \) | 7.1 |
| \( C_{w1} \) | \( C_{b1}/\kappa^2 + (1 + C_{b2})/\sigma \) |
| \( C_{w2} \) | 0.3 |
| \( C_{w3} \) | 2.0 |
| \( C_{t3} \) | 1.2 |
| \( C_{t4} \) | 0.5 |
9. Remarks
- The function \( f_{t2} \) is optional and often disabled in fully turbulent RANS.
- In SA-DES / DDES / IDDES, the wall distance \( d \) is replaced everywhere by a modified length scale.
- In SA-neg, the same formulation applies, but \( \tilde{\nu} \) is allowed to become negative with modified handling of \( f_{v1}, f_{v2}, f_w \).
Rotation correction
https://turbmodels.larc.nasa.gov/spalart.html#saR
Spalart-Allmaras One-Equation Model with Rotation Correction (SA-R)
\[ P_{\tilde{\nu}}= C_{b1} (1 - f_{t2}) (\tilde{S} + C_{rot}\min(0,|\sigma|-S)) \tilde{\nu} \]Where strain rate magnitude $|\sigma| = \sqrt{2\sigma_{ij}\sigma_{ij}}$ and strain rate is $\sigma_{ij} = 1/2(\partial_i u_j + \partial_j u_i)$.
Note that production is allowed to be negative here and the recommended coefficient is $C_{rot} = 2$.
Modified DES Length Scale
Shur, Mikhail L., et al. “A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities.” International journal of heat and fluid flow 29.6 (2008): 1638-1649.
The ψ-modified DES length becomes:
\[ d_{DES}= \min \left( d, \; \Psi \, C_{DES} \Delta \right) \]Enlarges LES scale to maximum 10x when $f_{t2}$ is active.
or, in DDES / IDDES shielding form:
\[ d_{DDES}= d- f_d \max \left( 0, \; d - \Psi \, C_{DES} \Delta \right) \]Very important note
ChatGPT says to replace only the denominator in destruction term as the DES length scale ($\frac{\tilde{\nu}}{\kappa^2 d^2}$). This is not completely right.
Ansys Fluent and OpenFOAM are confirmed to replace all wall distances in SA.Cylinder flow
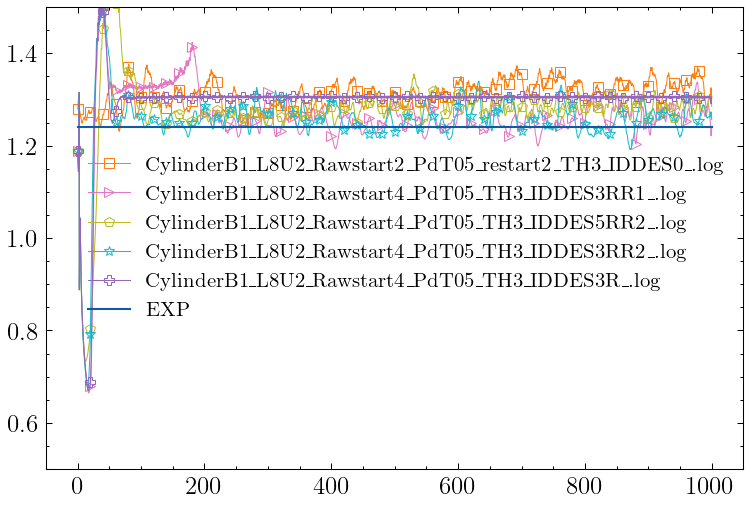
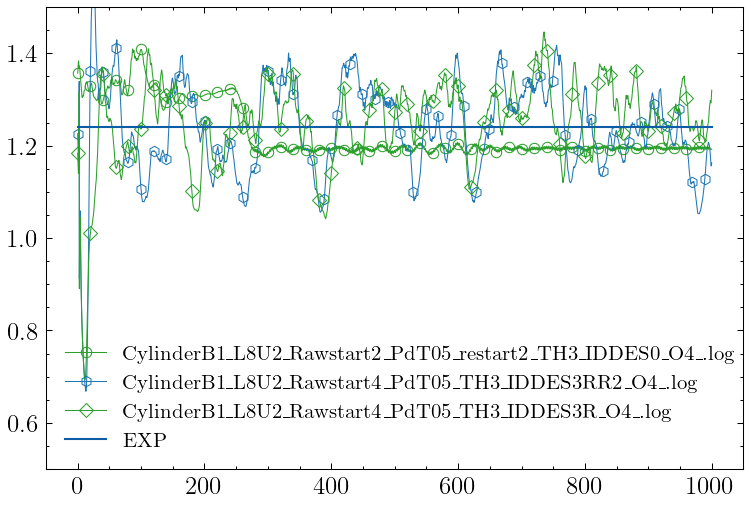
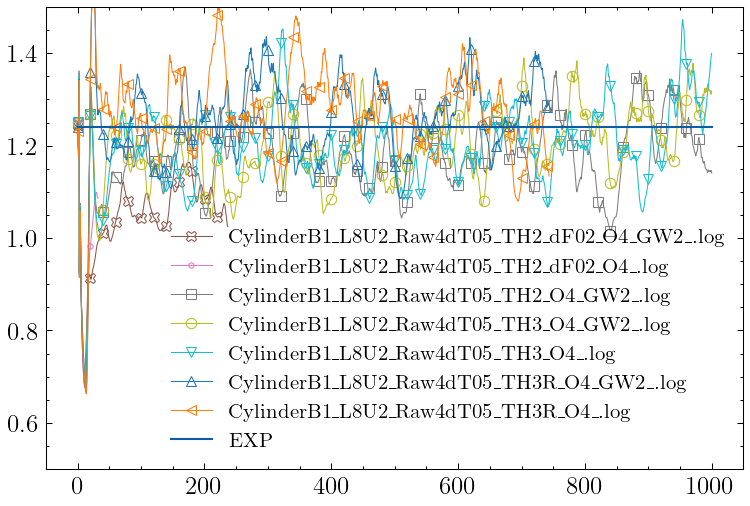
Re 5000, Ma 0.1.
Expected (Experimental) drag coef: 1.24 (4.96 in force for L=8)
CylinderB1 L8U2 mesh with ~1.09 million cells.
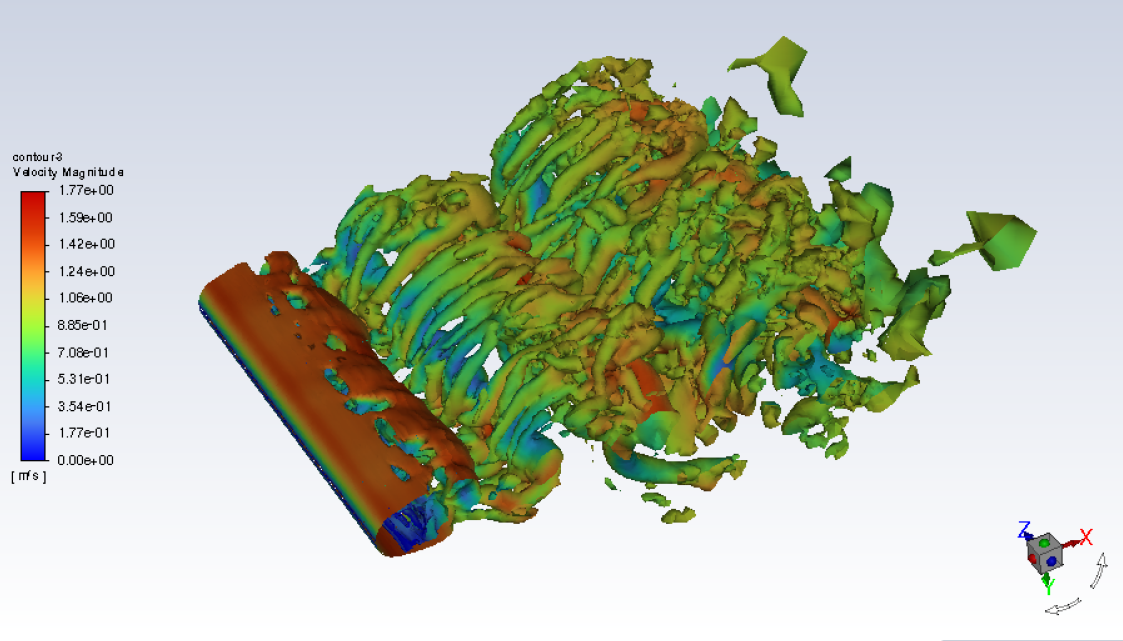
Visualizations



Partial vs. full DES length replacement
O2
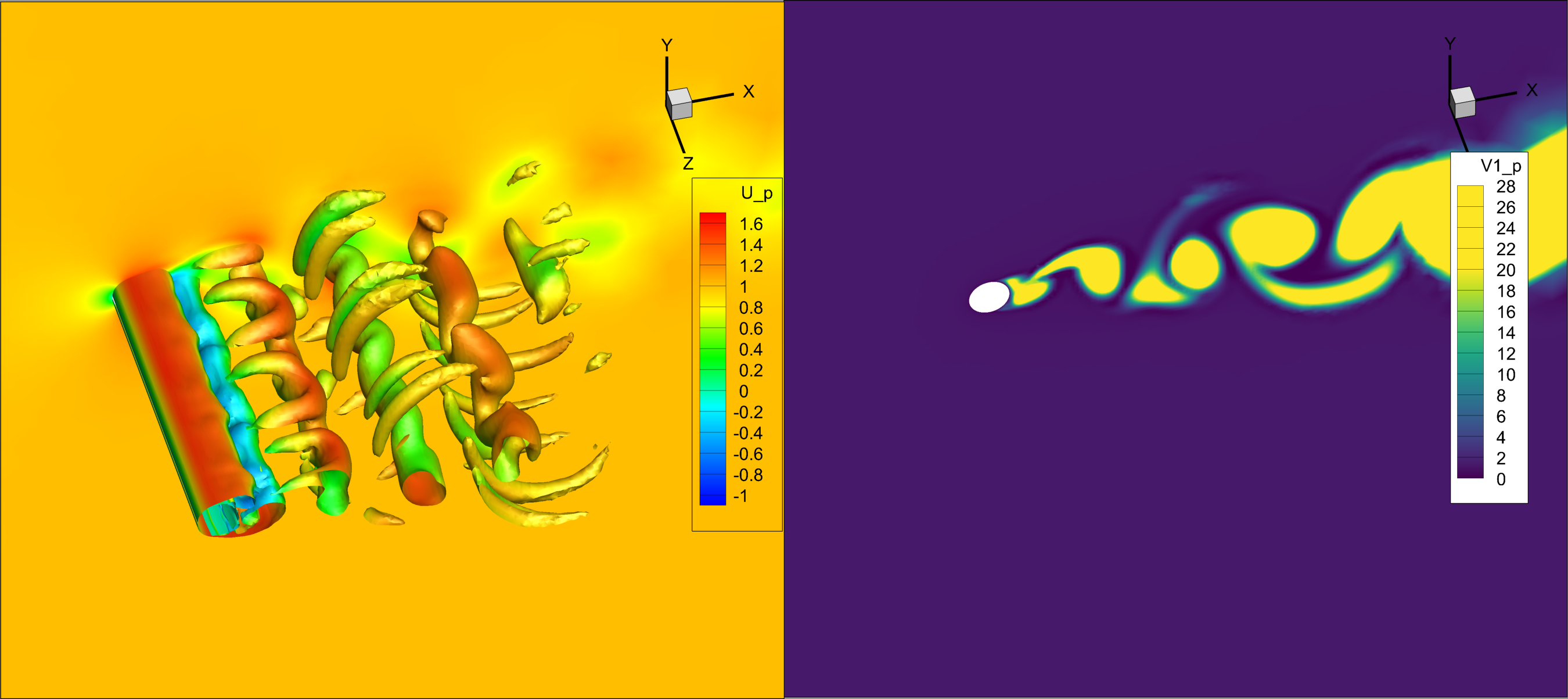
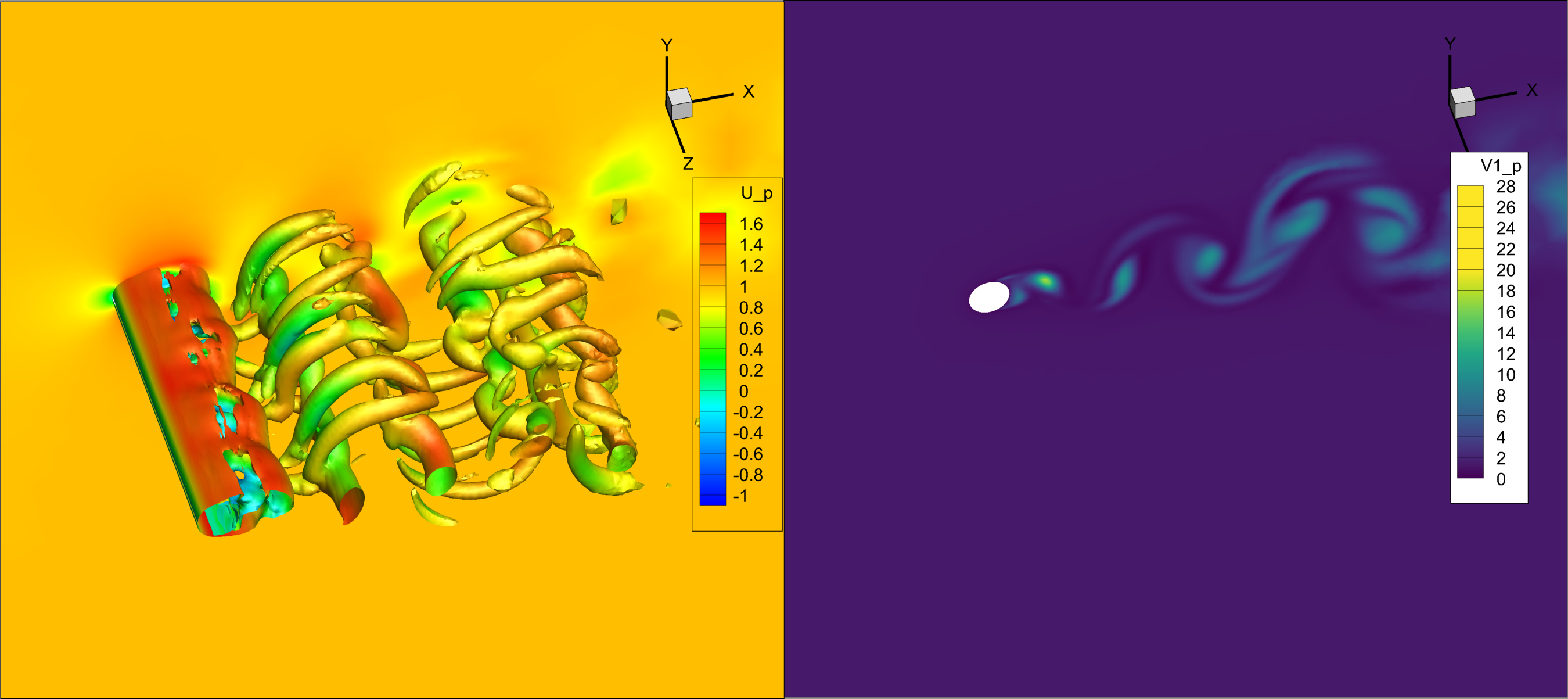
O4
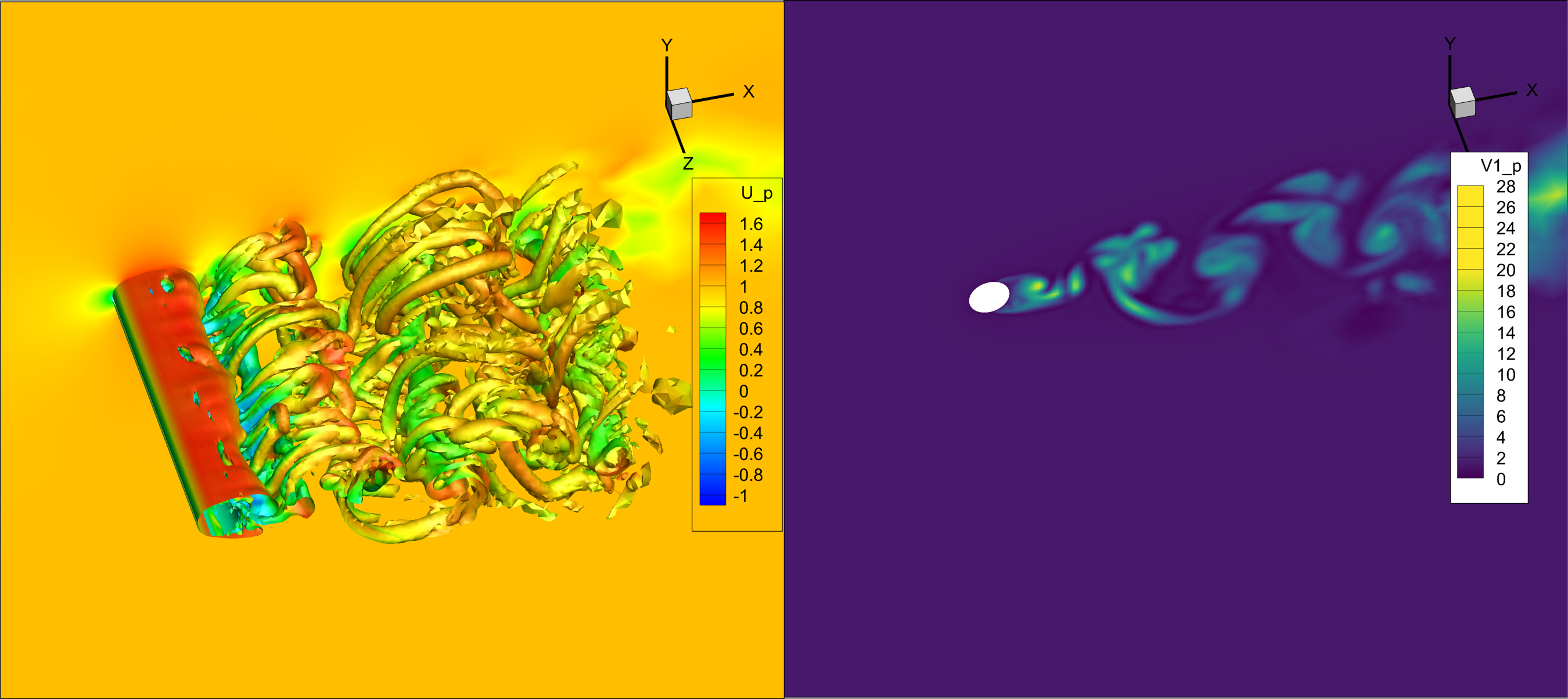
Partial vs. full DES length replacement
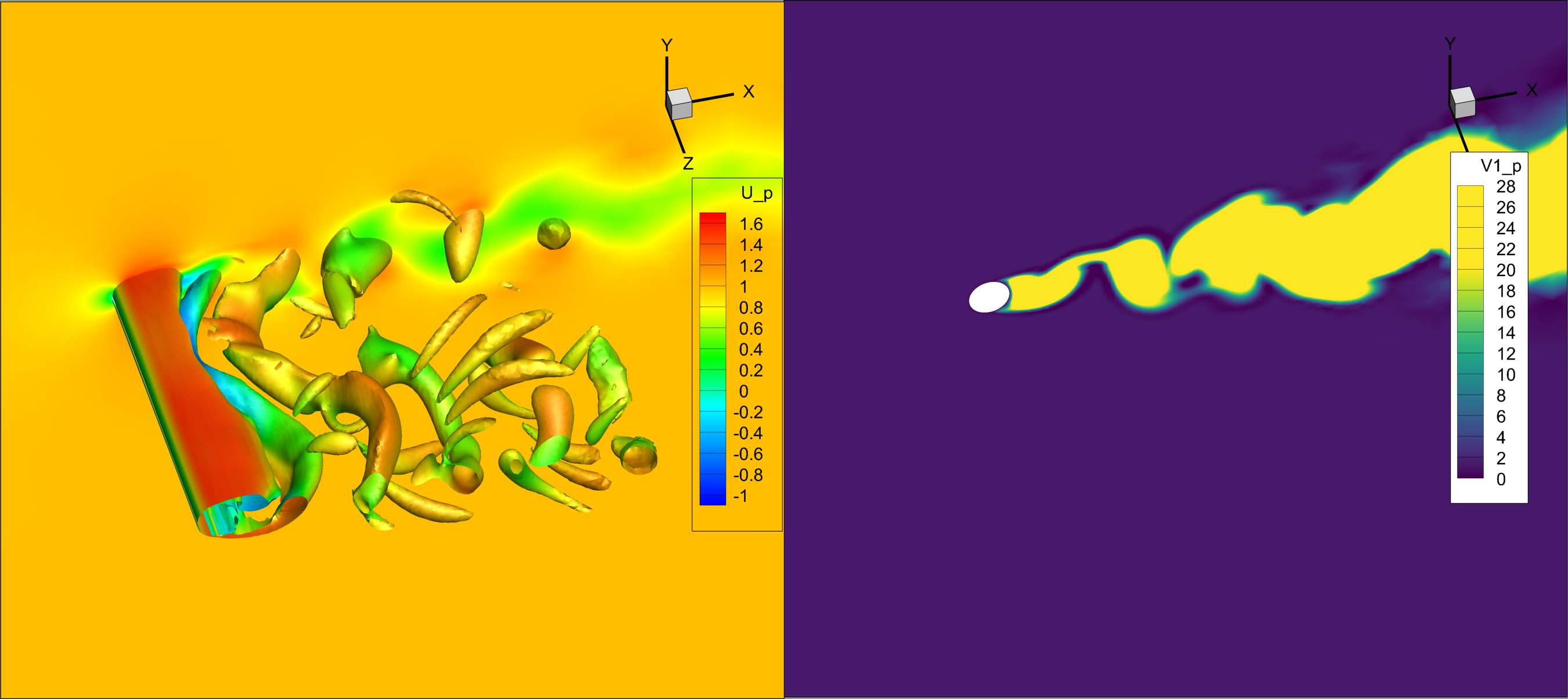
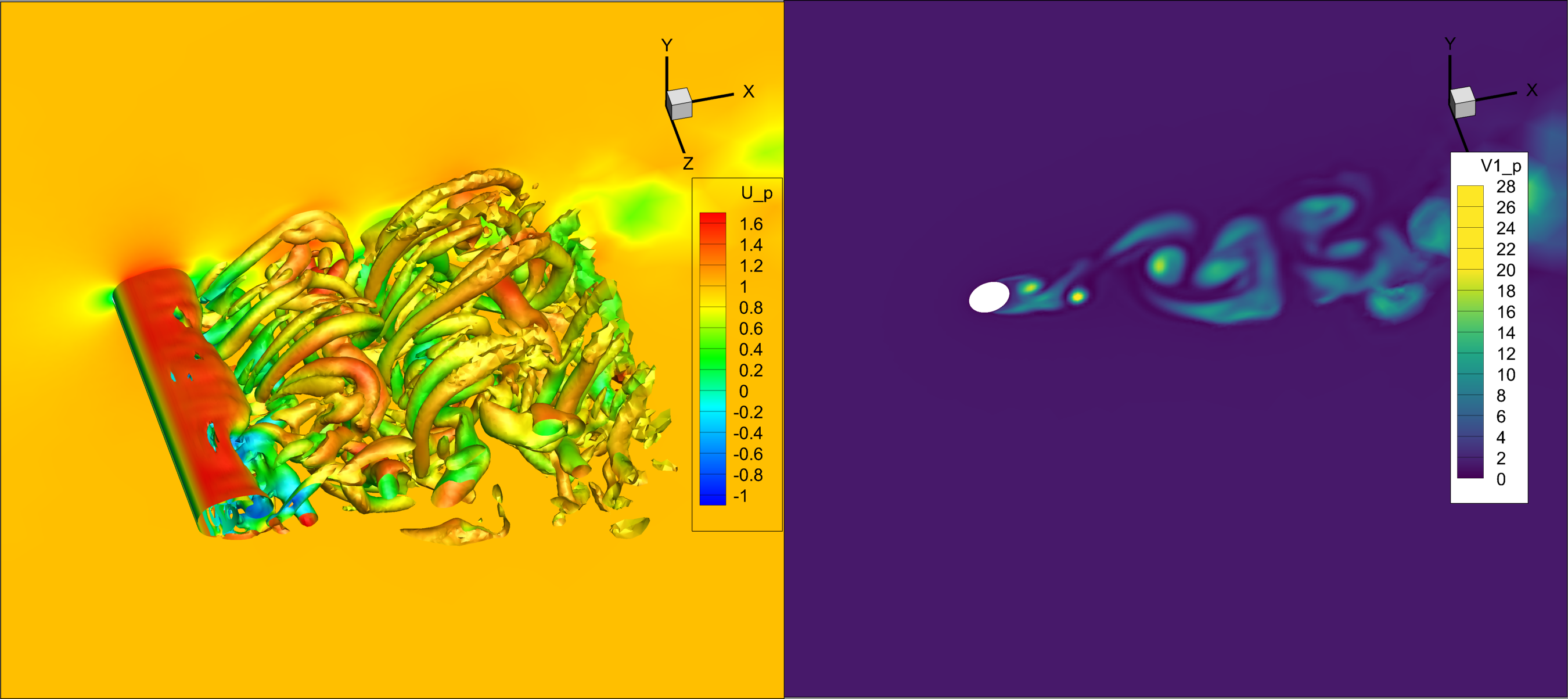
Full vs. modified upwind
$$ \hat F= \frac{1}{2}(F_L+F_R)-\frac{C_{dF}}{2}R|\Lambda|L(U_R-U_L) $$with $C_{dF}=0.2$.
O2
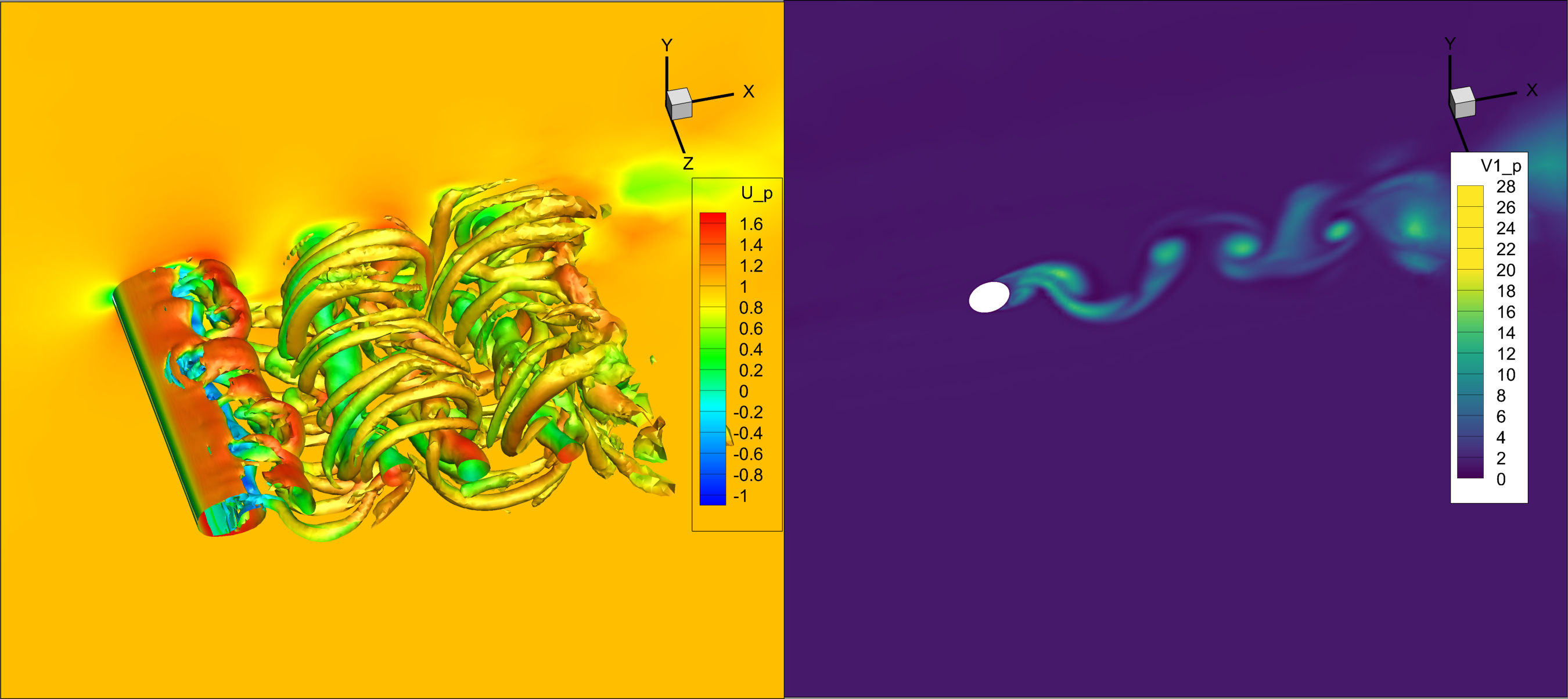
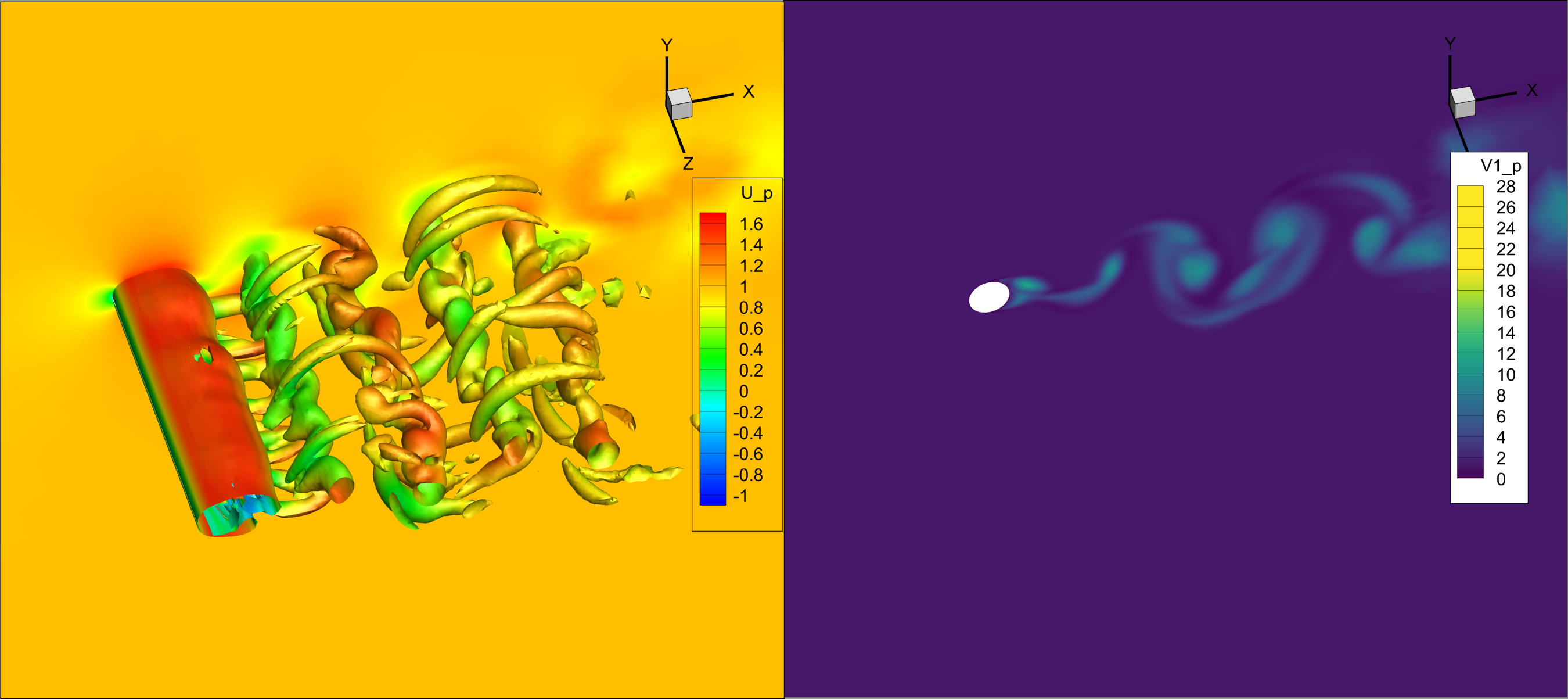
O4

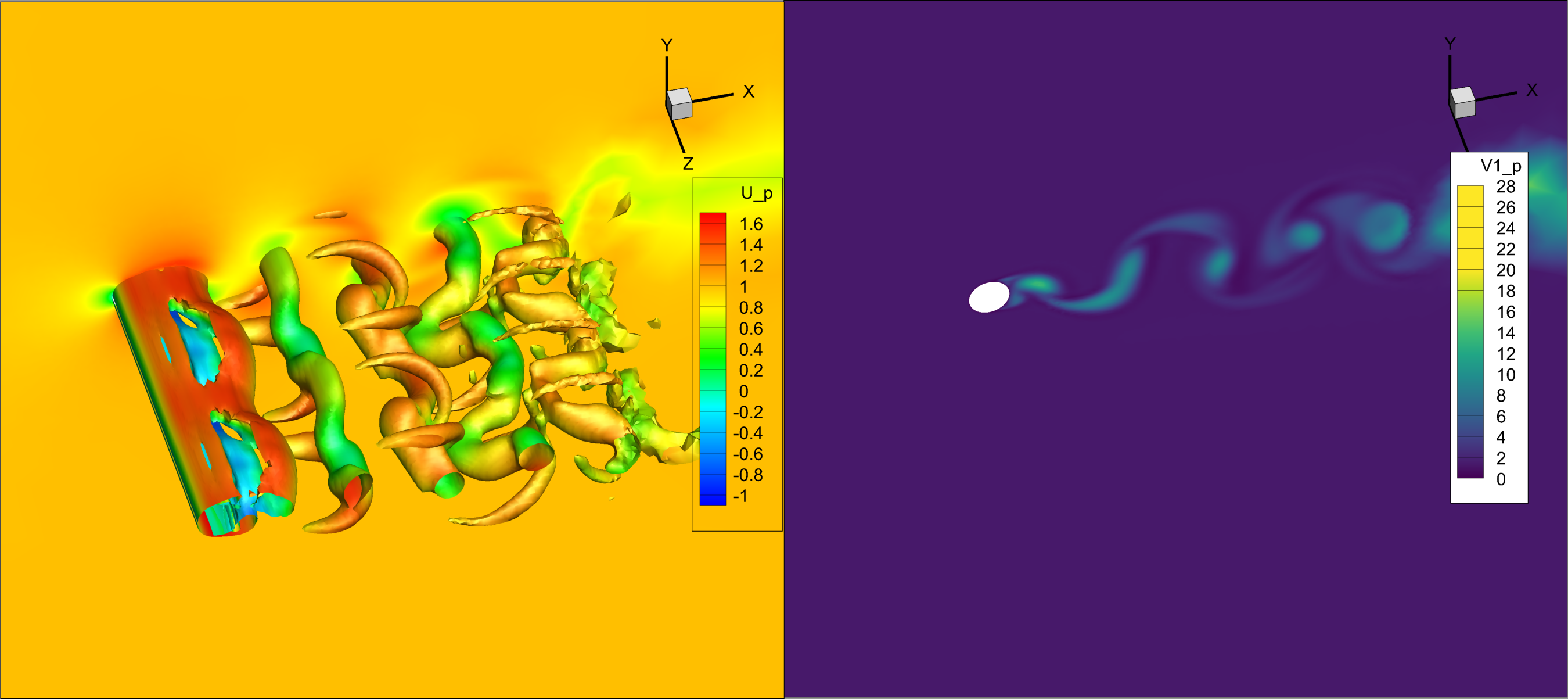
No $\Psi$ against $f_{t2}$

Others
(Wrong Rot correction)
Drag
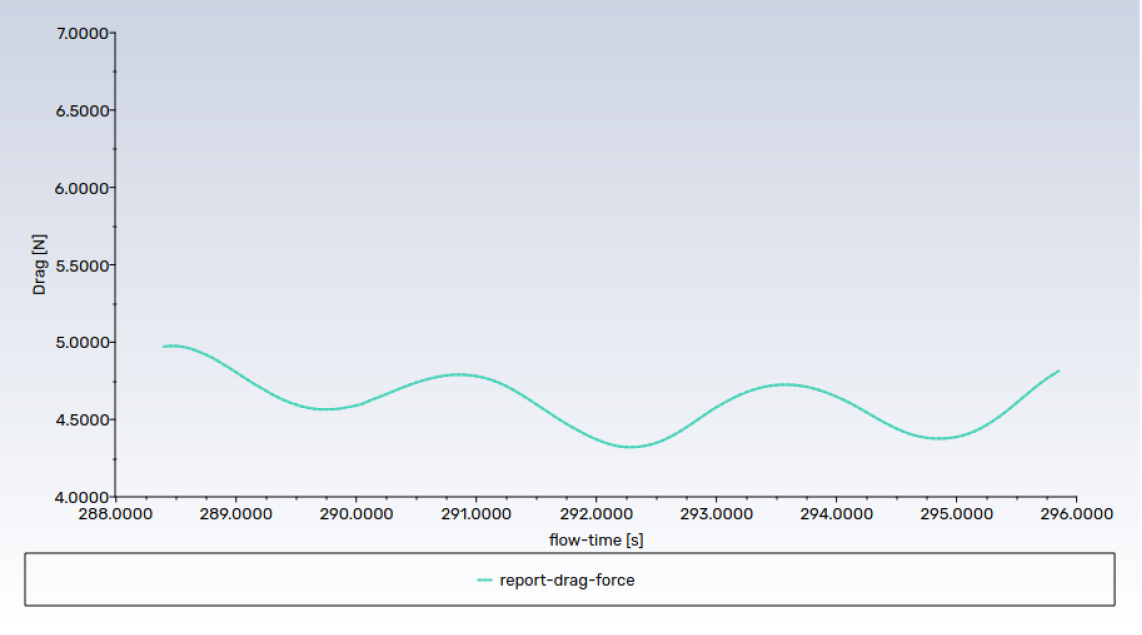
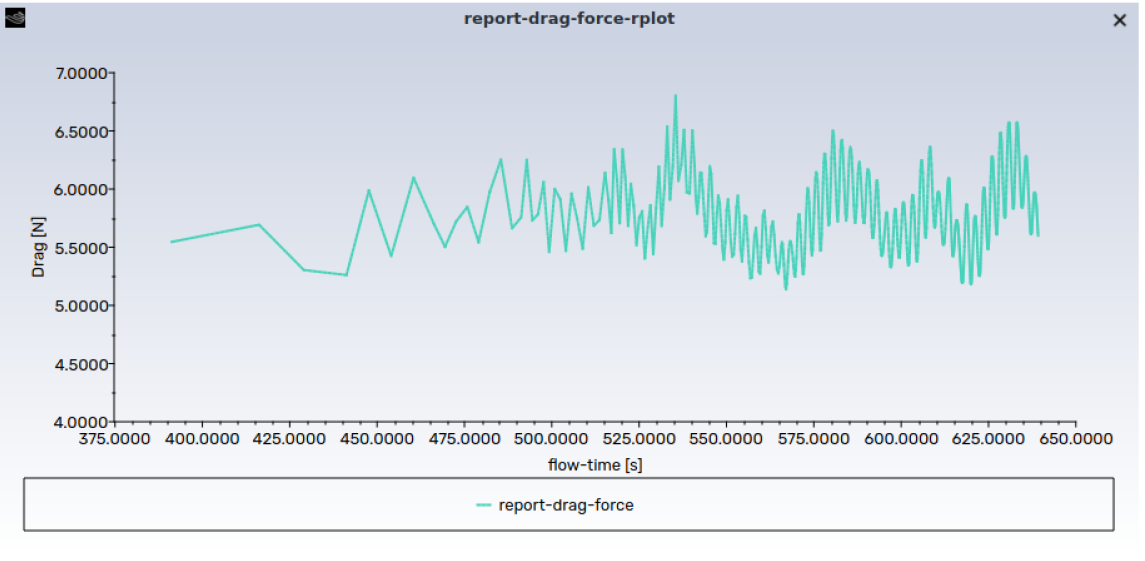
DNDSR drags
| Case | $C_d$ | error | i0 |
|---|---|---|---|
| CylinderB1_L8U2_Rawstart2_PdT05_restart1_TH3_.log | 1.3178e+00 | 777.6 | 18000 |
| CylinderB1_L8U2_Rawstart2_PdT05_restart2_TH3_IDDES0_.log | 1.3309e+00 | 909.3 | 18000 |
| CylinderB1_L8U2_Rawstart2_PdT05_restart2_TH3_IDDES0_O4_.log | 1.1945e+00 | -454.6 | 18000 |
| CylinderB1_L8U2_Rawstart3_PdT05_TH3_ILES_O4_.log | 1.0525e+00 | -1874.7 | 18000 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_ILES_dF02R_O4_.log | 1.0370e+00 | -2029.9 | 11607 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_ILES_dF02R_O4_GW2_.log | 9.8482e-01 | -2551.8 | 11942 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3RR1_.log | 1.2726e+00 | 326.0 | 18000 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3RR1_dF02_.log | 1.2477e+00 | 77.4 | 17586 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES5RR2_.log | 1.2855e+00 | 455.0 | 18000 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3RR2_.log | 1.2654e+00 | 253.9 | 18000 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3RR2_O4_.log | 1.2005e+00 | -395.1 | 17823 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3RR2_dF02_O4_.log | 1.1362e+00 | -1038.2 | 10520 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3R_O4_.log | 1.2586e+00 | 186.1 | 18000 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3R_dF02_.log | 1.2136e+00 | -264.4 | 17670 |
| CylinderB1_L8U2_Rawstart4_PdT05_TH3_IDDES3R_.log | 1.3048e+00 | 648.1 | 18000 |
| CylinderB1_L8U2_Raw4dT05_TH2_dF02_O4_GW2_.log | 1.0958e+00 | -1441.8 | 2739 |
| CylinderB1_L8U2_Raw4dT05_TH2_dF02_O4_.log | 9.4938e-01 | -2906.2 | 0 |
| CylinderB1_L8U2_Raw4dT05_TH2_O4_GW2_.log | 1.2364e+00 | -36.1 | 18000 |
| CylinderB1_L8U2_Raw4dT05_TH3_O4_GW2_.log | 1.2654e+00 | 254.1 | 18000 |
| CylinderB1_L8U2_Raw4dT05_TH3_O4_.log | 1.2876e+00 | 476.5 | 18000 |
| CylinderB1_L8U2_Raw4dT05_TH3R_O4_GW2_.log | 1.2706e+00 | 306.4 | 12820 |
| CylinderB1_L8U2_Raw4dT05_TH3R_O4_.log | 1.2178e+00 | -222.1 | 12871 |
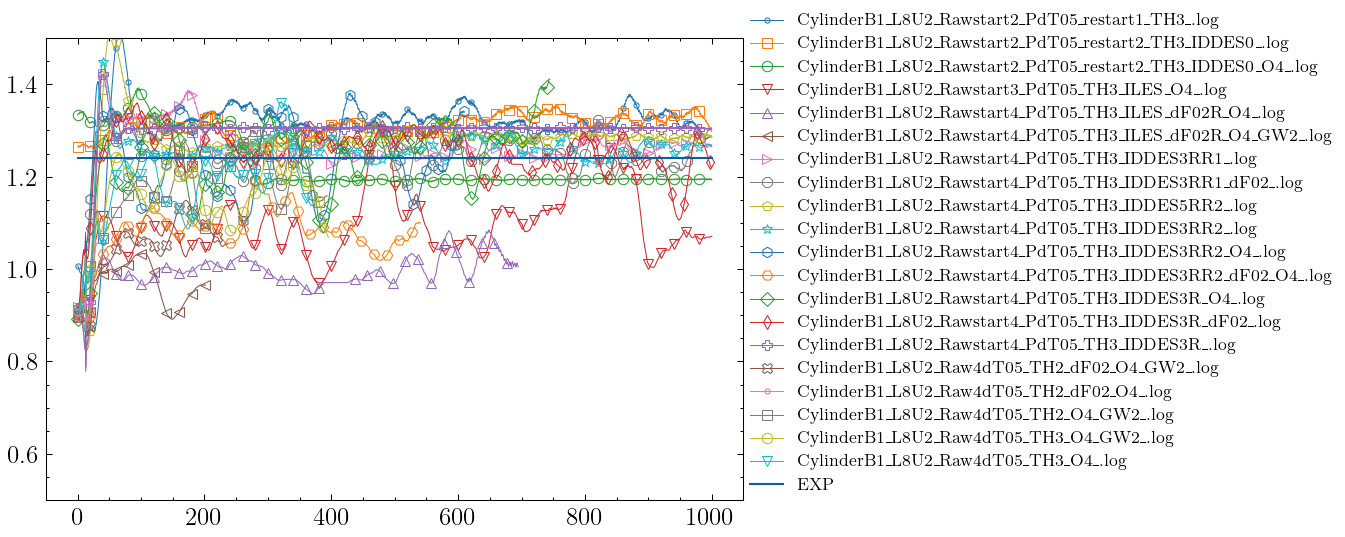
ILES results
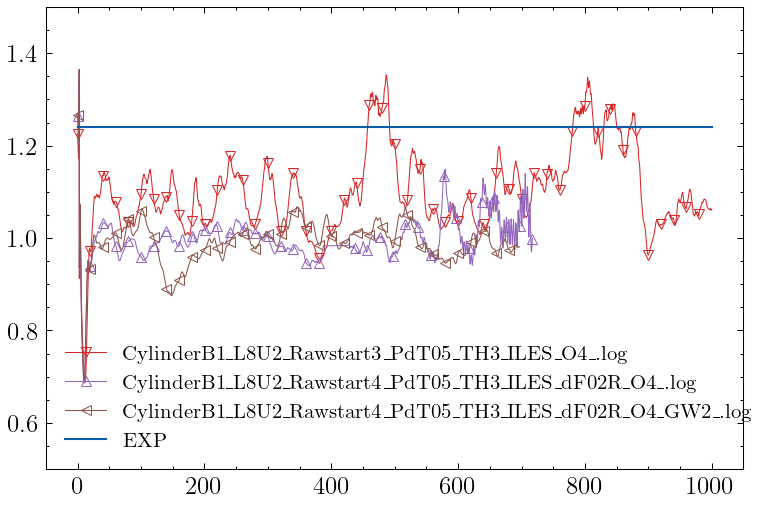
Different DES